시간복잡도(Time Complexity)
주어진 문제를 해결하기 위한 연산 횟수.
일반적으로 수행 시간은 1억 번의 연산을 1초의 시간으로 간주하여 예측한다.
시간 복잡도 유형
- 빅-오메가(Ω(n)): bset case의 연산 횟수를 나타낸 표기법
- 빅-세타(θ(n)): average case의 연산 횟수를 나타낸 표기법
- 빅-오(O(n)): worst case의 연산 횟수를 나타낸 표기법
시간 복잡도 계산
일반적으로 최악의 경우인 빅오 표기법을 사용한다
최고차항을 제외한 모든 항과 계수를 무시한다.
- T(n) = 3n^2 + 2n + 1 -> O(n^2)
시간복잡도 표기
O(1) - 상수 시간
O(logN) - 로그 시간
for(int i=0; i<=n; i*2){
...
}
i 값이 반복할 때마다 2배씩 증가. 이것을 k번 반복했을 때
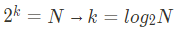
O(n) - 선형 시간
O(n^2) - 2차 시간
O(2^n) - 지수 시간

공간복잡도(Space Complexity)
- 알고리즘에서 사용하는 메모리 양
- 보조공간, 입력공간을 합친 포괄적인 개념
- 보조 공간은 알고리즘이 실행되는 동안 사용되는 임시 공간이므로 입력공간을 고려하지 않는다
공간 복잡도 계산
int sum(int a[], in n)
{
int x = 0;
for(int i=0; i<n; i++){
x = x +a[i];
}
return(x);
}
위 알고리즘은 4개의 변수를 사용하고 있다.
- int arr[n] : 4*n byte
- int n : 4 byte (입력 공간)
- int x : 4 byte (보조 공간)
- int i : 4 byte (보조 공간)

